P & NP

P: class of problems solvable in polynomial time. $O(n^k)$ for some constant $k$.

Shortest paths in a graph.
NP: class of problems verifiable in polynomial time.

Verifying a cycle is hamiltonian.
NP-complete: problem is in NP and is as hard as any problem in NP.

如果NPC问题可在多项式时间内被解决，那么所有的NP问题都可以在多项式时间内被解决

Interval Scheduling / 区间调度问题

Requests $1,2, . . . , n$, single resource

$s(i)$ start time, $f(i)$ finish time, $s(i) < f(i)$ (start time must be less than finish time for a request)

Two requests $i$ and $j$ are compatible if they don’t overlap, i.e., $f(i) \le s(j)$ or $f(j) \le s(i)$.

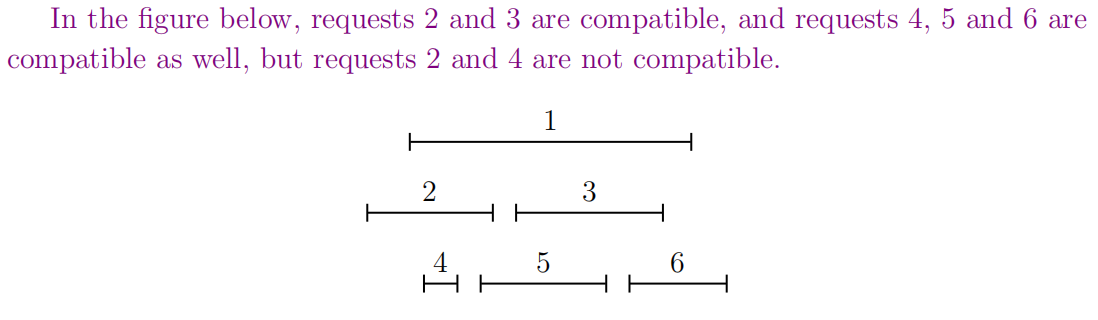
intervalScheduling

Goal: Select a compatible subset of requests of maximum size.

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。

Claim 1. Greedy algorithm outputs a list of intervals

$< s(i_1), f(i_1)>, < s(i_2), f(i_2)>, . . . , < s(i_k), f(i_k) >$

such that

$s\left(i_{1}\right)<f\left(i_{1}\right) \leq s\left(i_{2}\right)<f\left(i_{2}\right) \leq \ldots \leq s\left(i_{k}\right)<f\left(i_{k}\right)$

Claim 2. Given list of intervals $L$, greedy algorithm with earliest finish time produces $k^\ast$ intervals, where $k^\ast$ is optimal.

证明可使用数学归纳法，从$k^\ast=1$的base case归纳，可以得到$k^\ast$一直是最优的序列，详细过程略。

Each request $i$ has weight $w(i)$. Schedule subset of requests that are non-overlapping with maximum weight.

我们不难发现，在此时贪心算法是失效的，因此我们选择动态规划解决。

动态规划（DP）是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

我们这样定义Weighted Interval Scheduling的子问题：

$R^{x}=\{j \in R \mid s(j) \geq x\}$

其中，$R$是所有request的集合，如果我们令$x=f(i)$，那么$R^{x}$为集合$R$中起始时间晚于request $i$的request，这样我们需要解决的总子问题数$n=|R|$且只需要计算并记录一次。

当我们选择request $i$作为序列的起始时，那么剩余的request集合为$R^{f(i)}$，不难注意到有些request与request $i$是协调的，但它仍然不会出现在$R^{f(i)}$中，即我们在按序遍历所有的子问题：

$\operatorname{opt}(R)=\max _{1 \leq i \leq n}\left(w(i)+\operatorname{opt}\left(R^{f(i)}\right)\right)$

此时，时间复杂度为$O(n^2)$，这是由于解决每个子问题的时间复杂度为$O(n)$.

$f(1) \le f(2) \le ...\le f(n)$

于是我们可以得到更优的算法：

M[0] = 0
for j = 1 to n
	M[j] = max(w(j)+M[p(j)], M[j-1])