Paradigm

对于分而治之问题的时间复杂度计算：对于数据规模为$n$的问题，如果分解成规模为$\frac{n}{b}$的子问题，且$a\ge 1,b > 1$，那么有

$T(n)=a T\left(\frac{n}{b}\right)+[work\ for\ merge]$

我们会在下一节课通过Master Theorem得到具体的时间复杂度

Convex Hull

在平面中给定$n$个点，假定任意两个点的x坐标与y坐标都不相同，且没有三个点出现在同一直线上。

$S = \{(x_i, y_i)|i = 1, 2,...,n\}$

Convex Hull (CH(S)): 包含$S$中所有点的最小多边形

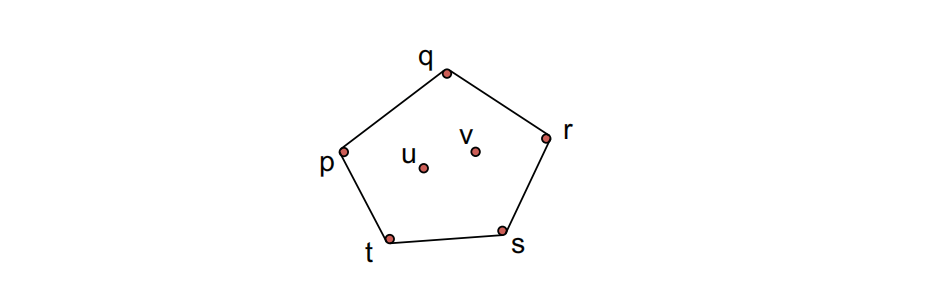
convex hull

CH(S)可以通过一个双向链表由边界上的点序列按顺时针顺序表示：

dot sequence

Brute force for Convex Hull

直接遍历每一条线段是否为CH(S)的一条边：

若其它所有点都在这条边的一侧，那么这条线段属于CH(S)
否则，则不是CH(S)的一条边

$O(n^2)$ edges, $O(n)$ tests ⇒ $O(n^3)$ complexity （怎样优化？）

Divide and Conquer Convex Hull

Sort points by x coord (once and for all, $O(nlogn)$)

For input set S of points:

Divide into left half A and right half B by x coords
Compute CH(A) and CH(B)
Combine CH’s of two halves (merge step)

How to Merge?

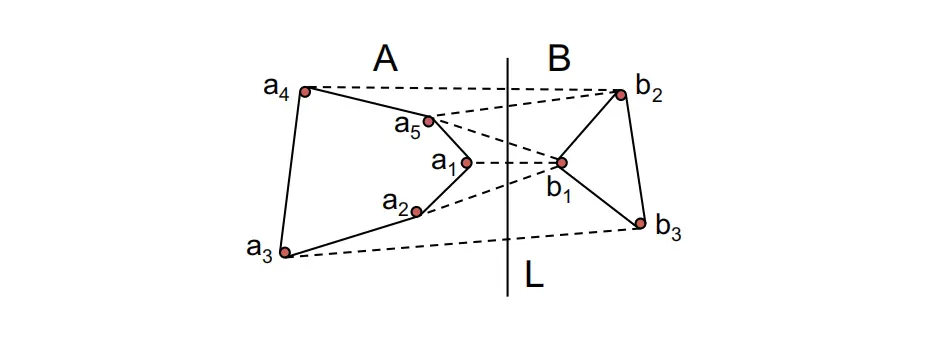
merge example

找到upper tangent $(a_i,b_j)$，在这里$(a_4,b_2)$即为U.T.
找到lower tangent $(a_k,b_m)$，在这里$(a_3,b_3)$即为L.T.
首先连接$(a_i,b_j)$，按照顺时针遍历B的链表直到$b_m$，连接$(a_k,b_m)$，同样的，以顺时针遍历直到A的链表直到$a_i$，这样我们就得到了新的Covex Hull

Finding Tangents

Assume $a_i$ maximizes x within CH(A) $(a_1, a_2,…,a_p)$. $b_1$ minimizes x within CH(B) $(b_1, b_2,…,b_q)$

$L$ is the vertical line separating A and B. Define $y(i, j)$ as y-coordinate of intersection between L and segment $(a_i, b_j)$

Claim: $(a_i,b_j)$ is uppertangent iff it maximizes $y(i, j)$. If $y(i, j)$ is not maximum, there will be points on both sides of $(a_i, b_j)$ and it cannot be a tangent

Algorithm: Obvious $O(n^2)$ algorithm looks at all $a_i, b_j$ pairs. $T(n)=2T(n/2)+ Θ(n^2) = Θ(n^2)$

i=1, j=1
while (y(i, j + 1) > y(i, j) or y(i − 1, j) > y(i, j))
	if (y(i, j + 1) > y(i, j)) -> move right finger clockwise
		j = j + 1(mod q)
	else
		i = i − 1(mod p) -> move left finger anti-clockwise
	return (a_i, b_j) as upper tangent

Median Finding

给定一个有n个数的集合，定义rank(x)为集合中小于等于x的数的数量，找到集合中第$\left\lfloor\frac{n+1}{2}\right\rfloor$大的数(lower median)与第$\left\lceil\frac{n+1}{2}\right\rceil$大的数(upper median). 通过排序来解决这样一个问题是显然的，但时间复杂度会达到$\Theta(n \log n)$，如何优化？

Select (S,i)

Pick x ∈ S cleverly
Compute k = rank(x)
B = {y ∈ S|y < x}
C = {y ∈ S|y > x}
if k = i
	return x
else if k>i
	return Select(B, i)
else if k<i
	return Select(C, i − k)

Picking x Cleverly

我们需要合理的选取x以防止极端情况出现：

将集合S分成大小为5的列（$\left\lceil\frac{n}{5}\right\rceil$列）
对每一列进行排序，时间复杂度为线性
找到每一列中位数的中位数

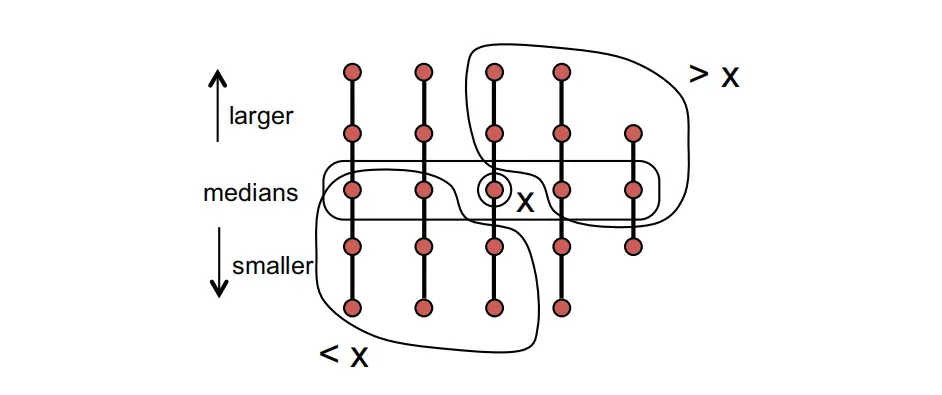
visual

有多少个数是保证大于x的？

至少一半的$\left\lceil\frac{n}{5}\right\rceil$列都会保证至少有3个数是大于x的，除了x所在的列与少于5个数的列，因此至少有$3(\left\lceil\frac{n}{10}\right\rceil-2)$个数大于x，于是有：

$T(n)=\left\{\begin{array}{ll}O(1), & \text { for } n \leq 140 \\ T\left(\left\lceil\frac{n}{5}\right\rceil\right)+T\left(\frac{7 n}{10}+6\right), \Theta(n), & \text { for } n>140\end{array}\right.$

证明递归复杂度过程略